Loi de Lévy
Loi définie par la
Densité : $$f_{\mu,c}:x\mapsto\Bbb 1_{x\gt \mu}\sqrt{\frac c{2\pi} }\frac1{(x-\mu)^{3/2} }\times e^{-c/2(x-\mu)}$$
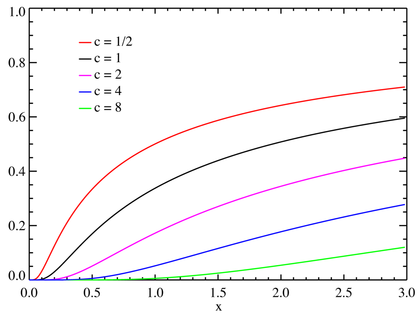
- particularité : possède une queue très lourde : \(f_{\mu,c}(x)\underset{+\infty}\sim\sqrt{\frac c{2\pi} }\frac1{x^{3/2} }\)